Challenges to Comprehension Implied by the Logo of Laetus in Praesens
Laetus in Praesens Alternative view of segmented documents via Kairos
25th April 2006 | Draft

Comprehension of Requisite Variety for Sustainable Psychosocial Dynamics

Transforming a matrix classification onto intertwined tori

-- / --

Introduction
From matrix to torus
Systemic sub-systems vs Preferred modes: "Columns" vs "Rows"
Generic matrix
Distribution of significance on torus surface
Interlocking tori: combining the two alternative representations
Dynamics of interlocked tori
Distribution of significance "within" a torus: using a third dimension for "Engagement with reality"
Contiguity of paired circular cross-sections
"Empty" centres and four-dimensionality
Psychosocial relevance of torus-related dynamics
Coherence, instability and failure of psychosocial systems
Resonant associations and comprehension of feedback vital to sustainability
Beyond the plane: form and medium in terms of the calculus of indications
Resonant association of psychosocial identity with intertwined tori
Memorability: musical clues to psychosocial system sustainability
Possible immediate applications of relevance to sustainability
Choosing the dimensionality of living
Potentially problematic consequences
References

Introduction

Systems of classification, whether described as nested thesauri or ontologies, necessarily take the form of nested lists. This approach is facilitated by the ease of representation in printed texts and the menu structure of standard software applications. Additional requirements and constraints are imposed on any classification that is organized as a matrix. This is a format typical of many academic papers where a list structure is viewed as inadequately modest in its dimensionality. The emphasis here is however on comprehension of psychosocial systems rather than descriptive explanation.

In the light of some use of matrix organizations of categories, the exploration here is extended to the projection of a matrix pattern of categories onto a single torus and onto several intertwined tori. This implies that some distinctions explicit there are only implicit or conflated in any representation in a simpler matrix or list.

The assumption here is that purely descriptive articulations, no matter how sophisticated the language used, lack the requisite variety to encompass the differences characteristic of psychosocial dynamics. However, efforts to "grasp" and "possess" higher-dimensional processes through their lower-dimensional "containers" misunderstand the nature of those processes and their relationship to the understanding vital to sustainability.

From matrix to torus

Ingetraut Dahlberg founded the journal International Classification (1974), which later became Knowledge Organisation (1993) and was the instigator in 1989 of the International Society for Knowledge Organization. In 1981 Dahlberg proposed a matrix-structured Information Coding Classification (ICC) as a universal classification scheme -- and represented it in 1996 (see discussion by Joseph T. Tennis, Layers of meaning: disentangling subject access interoperability, 2001). Dahlberg's early approach had been adapted for the classification of international organizations, the problems perceived by them, and the strategies advocated by them (cf Functional Classification in an Integrative Matrix of Human Preoccupations, 1982). This adaptation continues to be used, implicitly, as the basis for online access to the associated databases.

Questioning the limitations of a matrix representation, the possibility of using projection onto centro-symmetrical polyhedra was envisaged in 1980 (cf Needs Communication: viable need patterns and their identification, 1980) and explored in relation to the issues and strategies of the 1992 Earth Summit (Configuring Globally and Contending Locally: shaping the global network of local bargains, 1992; Spherical Configuration of Categories to Reflect Systemic Patterns of Environmental Checks and Balances, 1994). The approach taken in what follows advocates a different step in integration by transforming the matrix into a torus, as notably fundamental to the organization of computer memory for parallel processing, especially in supercomputers [more | more] . The process is described in MathWorld as follows:

An (ordinary) torus is a surface having genus one, and therefore possessing a single "hole"... The single-holed "ring" torus is known in older literature as an "anchor ring." It can be constructed from a rectangle by gluing both pairs of opposite edges together with no twists... The usual torus embedded in three-dimensional space is shaped like a donut, but the concept of the torus is extremely useful in higher dimensional space as well. [more]

The projection of a matrix onto a torus is achieved in two distinct ways:

Transition from matrix to torus
Transition from matrix to torus Transition from matrix to torus Transition from matrix to torus

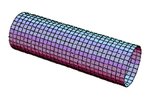The two approaches are of course geometrically equivalent. The form raises interesting questions regarding:

The general concern here is with the challenge to richer comprehension and how it needs to match match the complexity of policy-making -- especially when different factions prefer to order their understanding of complex systems in different ways.

Systemic sub-systems vs Preferred modes: "Columns" vs "Rows"

The design of the matrix -- used notably for the databases of the Encyclopedia of World Problems and Human Potential -- benefitted from the insights of Erich Jantsch (The Self-organizing Universe: scientific and human implications of the emerging paradigm of evolution, 1980). Like that of Ingetraut Dahlberg, the adaptation highlighted the "levels" of human preoccupation from the extremely concrete to the extremely subtle -- represented by successive rows in the matrix. The various preferred approaches to reality (discussed below) constituted the columns of the matrix.

Engagement with reality: There is always a case for looking more attentively at the manner in which humans attend to their reality -- the manner of their cognitive engagement with it. This can of course vary from extremely concrete modalities to those of the subtlest, existential forms of identification with the environment. A distinction is however made here between:

The argument here is that any adequate descriptive modelling of a complex psychosocial system will include both sets of processes as sub-systems. On the other hand the two are readily conflated so that vital distinctions are lost -- reinforcing patterns of confusion. This typically occurs when the subjective dimension is considered irrelevant or denied. However it is also the case that the objective dimension may be denied, considered irrelevant, or treated as secondary, in the light of other understandings.

Preliminary objective approach: The emphasis in the first matrix / torus to be discussed initially is therefore on the sub-systems that lend themselves to more objective description, potentially acceptable even to the behavioural sciences. More subjective distinctions are discussed below in relation to a third dimension..

The emphasis here is however not so much on what the distinctions are (in terms of content), nor on how many should be made, but rather on the need to make a sufficient number in order to reflect diversity to an adequate degree (in accord with Ashby's Law of Requisite Variety). It is difficult to make rich music with a monochord unless it is --- It is equally difficult to make music with an instrument with a wide range of variants (as on an organ). The art is to select a sufficient number to be useful and comprehensible -- recognizing that the distinctions are being made in a continuum. The same applies to the variety of modes (columns) through which reality is engaged to whatever degree (as represented by the rows). Visually the point is made by the fret structure of a stringed instrument such as a guitar or a violin. The complexity of the structure needs to be sufficient for the music but not too challenging for the player or the audience. A sitar represents an extreme of complexity open only to the few.

Preferred modes ("columns") : Here the approach advocated is to take account of various conventionally preferred "ways" of making such distinctions. These could be understood as corresponding to different worldviews -- each understood to be complete in its own right. Without at this stage endeavouring to reconcile the differences between sets of approaches, the following sets are indicative of the ways in variety is distinguished:

Systemic sub-systems ("rows"): Here the distinctions relate to the way in which the psychosocial system is understood to work. Given any preference for a "mode" or "way" of understanding, the systemic sub-systems distinguished may be labelled in quite different ways. From a systemic or cybernetic perspective the sub-systems must necessarily work together as a system and their distinct functions are necessary for the viability of that system. The distinctions in question are however made in various ways, whether or not those distinctions are conflated under certain circumstances. An obvious example is the distinction between the basic computer operating systems (Macintosh, Windows, and Linux), and the associated worldviews, notably as highlighted by Eric S. Raymond (The Cathedral and the Bazaar, 1997):

Generic matrix

In the light of the above, it is possible to point to the existence of what might be termed a generic matrix

Indications of structure of a generic classification of knowledge
. . Indicative "columns"
. Biases B1 B2 B3 B4 B5 B6 B7 Bn
. Types T1 T2 T3 T4 T5 T6 T7 Tn
. Yogas Y1 Y2 Y3 Y4 Y5 Y6 Y7 Yn
. Intelligences I1 I2 I3 I4 I5 I6 I7 In
. Disciplines D1 D2 D3 D4 D5 D6 D7 Dn
. etc . . . . . . . .
Indicative "rows" . . . . . . . . . .
Haskell Cybernetics etc . Generic P1 P2 P3 P4 P5 P6 P7 Pn
H1 C1 . . S1 . . . . . . . .
H2 C2 . . S2 . . . . . . . .
H3 C3 . . S3 . . . . . . . .
H4 C4 . . S4 . . . . . . . .
H5 C5 . . S5 . . . . . . . .
H6 C6 . . S6 . . . . . . . .
H7 C7 . . S7 . . . . . . . .
Hn Cn . . Sn . . . . . . . .

From an abstract cognitive systemic perspective, it could be argued that distinct modal preferences ("columns") and the distinction of sub-systems ("rows") could be conflated together into a single set of more abstract distinctions -- an archetypal list of complementary insights (typical of pantheons, etc). Splitting them into two sets interwoven as a matrix however makes them more accessible to comprehension. A matrix cell at any point of intersection then holds insight that is more specifically and readily comprehensible. It also draws attention to aspects which might be readily neglected in any exposition of a particular preferred mode ("column") or in discussion of a particular systemic sub-system ("row"). Note that in the generic presentation above, the number of rows or columns may be decided by convention or preference.

Distribution of significance on torus surface

Corresponding to the two modes noted above, significance may be distributed in either of two ways:

Earlier examples of the possibility of knowledge organization on a torus include:

In considering the question of the number of distinctions it is useful to make with regard to columns and rows, it is appropriate to note the mathematical constraints relating to the colouring of a torus. The torus coloring of an ordinary (one-holed) torus requires 7 colours (consistent with the Heawood conjecture).

Interlocking tori: combining the two alternative representations

The two possible modes of representation may be represented together in a manner which holds a higher degree of complexity, raising interesting questions and possibilities. This is achieved by projecting each matrix (Mode A and Mode B) onto a separate torus in the manner discussed. The two tori are then allowed to interlock as illustrated by the following

Interlocking Tori
Version from Mathematica (wolfram.com)
Also versions in virtual reality (static / dynamic) 		Serrated variant in a sculpture design
by Carlo Sequin inspired by Keizo Ushio
Interlocking Tori Interlocking Tori

In the above representations the interlocked tori are of equal dimensions and have contiguous surfaces. This condition is the subject of further discussion below. However such interlocking may involve tori of quite unequal dimensions such that the surfaces do not touch or that one tube is of smaller radius than the other (whether or not they touch). Mathematica provides numerous examples. These point to the use of such differences to hold other kinds of significance concerning the relative emphasis placed on one representation or the other.

Dynamics of interlocked tori

Rather than assume that the two tori are simply static representations of sets of categories, there is a strong case for taking account of the dynamics associated with many occurrences of a torus in natural phenomena -- from smoke rings, through plasma containment in fusion reactors, to the environment of black holes. Anything defining the surface of a torus may then have two dynamics: (a) around the tube of the torus *** rotation***, (b) along the tube of the torus.

Give that such dynamics may occur in both tori when interlocked, interlocking is most smoothly achieved when the direction of the dynamics in each is such as to be mutually reinforcing. In effect the dynamics around the tube of one reinforces the dynamics along the tube of the other. If the tori are understood to be serrated, as in the aesthetic representation above, then the serrations effectively function like the teeth of gears at the interface between the two tori.

With respect to the cognitive content of the two matrices interrelated in this way, it can then be recognized how in a dynamic situation the "preferred modes of knowing" (potentially emergent within any psychosocial system) interact with the "sub-systems" variously perceived as important (to understanding and ensuring the operation of any psychosocial system) -- through the dynamics of the changing contact at the interface of the two tori.

When, as noted above, the dimensions of the torus are different, their relationship may reflect cognitive challenges corresponding to those the Kama Sutra delights in articulating through euphemism -- regarding the relationship between partners of different dimension: males (as rabbit, bull or horse) and females (as doe, cow or she-elephant) [more].

Screen shots of a dynamic virtual reality model of intertwined tori
(click on each variant to access and manipulate in 3D;
in the free Cortona VRML viewer, right click for preferences to switch from/to the "wireframe" presentation)
Dynamic virtual reality model of intertwined tori Red torus has a vortex (smoke ring) dynamic in the model 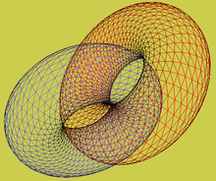interlocked tori wireframe interlocked tori with faces
Blue torus has a wheel-like dynamic in the model
VRML animations by Bob Burkhardt; variant kindly developed by Sergey Bederov of Cortona3D (interactive 3D version

Distribution of significance "within" a torus: using a third dimension for "Engagement with reality"

In the process of making the distinction above between "preferred modes" and "sub-systems", the possibility of a third dimension was noted. This concerns the degree of experiential ("subjective") engagement with "reality" as framed by the first two dimensions. It might be understood as the "maturity" or "depth" of response to objectively described systems and the degree of cognitive identification with them or "detachment" from them. This is important to any understanding of identity within such a system and for understanding the status of any perceived or conceived system in relation to the perceiver.

The suggestion here is for a classification that ranges::

Some approaches to this range include:

The elements of such a range may then be understood as corresponding to positions along the radius of the tube of either torus such that concentric circles around the centre of the tube (centred on its axis) correspond to different levels of insight. The cross-section then corresponds to the radial, centro-symmetric organization characteristic of many traditional mandalas [more]

The junction between the two interlocked tori may then be associated with a "deeper" or "more superficial" level of meshing. The surfaces of the tori may then be understood to "interpenetrate" corresponding to the level of insight in operation -- rather than interfacing at the "outer" surface as suggested by the above illustrations. One interestingly relevant representation of interlocking is based on an optical illusion by a random dot stereogram (see Two interlocking toruses).

Contiguity of paired circular cross-sections

There are three unique points of particular interest at the interface between the two interlocked tori on the line linking the axial centres of their respective rings -- effectively the line representing the junction between the planes of the two tori. In each case, it is the point at which the circular cross-section of one torus tube is contiguous with the circular cross-section of the tube of the other. The circular cross-sections are however orthogonal to one another -- the planes of the torus tube cross-sections are at right angles to each other.

The "twisted" surface connection bears some resemblance to a figure-of-eight or Möbius strip -- but with a second such loop, given that there are four such circles.

"Empty" centres and four-dimensionality

A torus is characterized by two types of "centre" that may, in respect of any cognitive mapping, be understood as "empty":

From a cognitive perspective such "empty" centres may be related to zones of cognitive "emptiness" that are a typical focus of spiritual disciplines. John Fudjack and Patricia Dinkelaker (The Enneagram as Classic 'Double Mandala', 1999) clarify the manner in which mandalas wrap through their centre to form a torus, reconciling two incommensurable orders of awareness - the undifferentiated and the differentiated:

In 'The Enneagram as Mandala' we sought to show that mandalas may be conceived as having a special kind of non-linear organizational form that we call 'liminocentric', in which the center of the structure wraps back around on the structure's periphery - so that its innermost and outermost reaches are identical in their 'undifferentiated' vastness, while intermediary levels are discrete and distinguishable. The two incommensurable orders of existence are thereby reconciled, and the mandala succeeds in representing what Jung called the 'Self'.

... liminocentric structuring is combined with a very special kind of paradoxical 'movement', a primordial sistolic/diastolic movement of consciousness, in which awareness alternately (and ultimately simultaneously) contracts inwardly toward the center of the diagram and back outward toward the periphery, in a manner that is most aptly modeled by a three-dimensional 'spiral' made to wrap back around on itself in a donut-shaped figure that is called a 'torus' by mathematicians. Mastery of this kind of mental movement is, as we shall see, the primary subject of the early 'Yoga Sutras', which act as the theoretical foundation for the meditational systems out of which the mandala, as a profound spiritual practice and visualization, originally emerged....

When, by using the torus, we move into the realm of three-dimensional figures, we find a more elegant solution than was available in our two dimensional spiral diagram, as the center appears no longer as a mere inner 'end point', but as an extended channel through which one can pass directly to the 'other side' of the figure.

Also of interest is that in the two interlocked tori there are four such zones of "emptiness" (along the plane of intersection) -- two associated with the respective axial rings and two associated with the respective tubular centres. In four dimensions these may be understood as unseparated and potentially having a common focus. This points to the possibility of understanding life and identity as a dynamic in 4 dimensions. On this point note the work of Walter J Freeman (Strange Attractors that Govern Mammalian Brain Dynamics Shown by Trajectories of Electroencephalographic (EEG) Potential, 1988) indicating that the strange attractor may also have the structure of a 2-torus, that fluctuates in size and shape aperiodically -- described as "a torus that breathes".

The dynamics along and around the tube of one torus, particularly as driven by the other, point to a particular condition at the circular cross-section where they are contiguous. This could be understood as constituting a third torus dynamic -- in relation to the "empty" centre at the axis of the tube at that point. This torus may be understood as arising from of curving the radial columns holding categories of "engagement with reality" to leave the axial centre free. The row dimensions then result from of the dimensions along the tube of the torus.

There are therefore two such "inner" tori each located within one or other of the two original tori at their point of contact *****.

Psychosocial relevance of torus-related dynamics

The torus has emerged as a focus of attention in the study of the non-linear dynamics of complex systems. A torus attractor occurs when there is coupled motion of an oscillating pair. As a dynamical system increases in complexity, it shifts from fixed point, to limit cycle, to torus attractor. However, with further complexity, the system breaks into chaotic movement and a new attractor, the strange attractor, emerges.

In a discussion of "integral awareness and the initial maturity of planetary civilization", Duane Elgin (Awakening Earth: exploring the evolution of human culture and consciousness, 1993) discusses an eighth dimension of societal development characterized by a "dynamically stable, self-referencing and self-organizing species-civilization" associated with a "wisdom-culture" within which polarities are effectively balanced "integrated continuously into a higher synthesis... comparable to a controlled chain reaction in a nuclear reactor...forever pulsing with creative life energy". He notes the unique value of the torus in modelling the associated process understanding:

To create a dynamic torus, two flows that would otherwise rapidly dissipate become self-containing of one another. Each flow brings focus and coherence to the other, and together they create a self-perpetuating, flow-through process that has the ability to endure as a stable system. In a similar way the material and consciousness aspects of life are mutually focusing and reinforcing of one another in a dynamic process... Our challenge is to "get ahold of ourselves" by integrating the material and consciousness aspects of life into a self-bounding process that is dynamically drawn from, and exists within, the meta-universe."

With respect to the torus, Elgin adds:

Despite the seeming simplicity of its structure, the torus embodies two paradoxical attributes consistent with our complex, flow-through nature: we are both dynamically closed (as self-organizing and self-bounding systems) and dynamically open (directly connecting with the meta-universe)... The flowing construction of the torus enables us to explore the crucial distinction between "consciousness" and "awareness"... the term awareness is used here to describe direct knowing, while the term consciousness is used to refer to a reflective process that stands apart from, and has some object of knowing.... A toroidal geometry also provides a way to visualize the convergence of Eastern and Western views of reality.

Despite the elevated stage of consciousness that Elgin's eighth stage represents, he stresses its direct link to contemporary experience citing the Zen saying "After awakening, we sweep the floor", namely the recognition of the "extraordinary nature of the reality that surrounds us", the "ordinary miracles of everday life", and the "progressive simplicity of living". This recalls his earlier exploration Voluntary Simplicity (1981/1993).

Subsequently Elgin (The Self-Guiding Evolution of Civilizations, 2002) notes that:

At every level of the cosmos, we find the characteristic structure and geometry of toroidal forms. The torus is significant because it is the simplest geometry of a dynamically self-referencing and self-organizing system that has the capacity to keep pulling itself together, to keep itself in existence. The most common signature of self-organizing systems in nature is the torus.

Elgin distinguishes six unique properties of self-organizing systems:

The organization of psychosocial dynamics -- especially nonlinear psychodynamics -- in terms of a torus has been explored in a number of ways:

Such literature typically focuses on the description and explanation of psychosocial dynamics through use of a torus -- or how the torus is a form natural to cognitive coherence within the brain. Such descriptions should however be considered quite distinct from the process of conscious comprehension of such dynamics -- namely how categorized psychosocial phenomena are ordered and remembered. In the approach taken above, emphasis was therefore placed on the function of:

The argument here is that purely descriptive articulations, no matter how sophisticated the language used, lack the requisite variety to encompass the differences characteristic of psychosocial dynamics -- whether or not some of these are condemned as "irrational" or "misguided". There is a need to embody "incommensurable" models as is done, for example, in the case of "competing" modules in voice-to-text transcription software.

A very interesting collective experiment with such necessary diversity was undertaken by the Institute of Cultural Affairs interrelating: economic processes and dynamics, political processes and dynamics, and social processes and dynamics (see Jon and Maureen Jenkins. Social Process Triangles, Imaginal Training, 1997; also Collective strategy-making: designing a strategic array, 1995). This work of the Institute of Cultural Affairs was associated with an ambitious articulation of psychological conditions in collaboration with the Ecumenical Institute (Jon and Maureen Jenkins, The Other World). An effort was made to integrate both approaches into the Encyclopedia of World Problems and Human Potential.

Coherence, instability and failure of psychosocial systems

In endeavouring here to interrelate typically incommensurable perspectives and understandings, the challenge is one of achieving higher orders of coherence. The most characteristic phenomenon undermining such coherence is a form of oscillation between polarized extremes under conditions which may indeed have a degree of stability to them but may well decay into a chaotic condition. The challenge of sustainability in psychosocial systems may be understood in such terms.

Astrophysics has drawn attention to the importance of the phenomenon of invariant tori in ensuring the stability of the orbit of a planet, such as Earth, which is subjected to destabilizing gravitational influences from a planet such as Jupiter with 10,000 times its mass. The orbit of Earth remains stable because it is in fact a torus [more]. This understanding arises from what is known as the Kolmogorov-Arnold-Moser theorem regarding dynamical systems with respect to the persistence of quasi-periodic motions under small perturbations. The motion is confined to a doughnut-shaped surface, an invariant torus

The recent developments of chaos and complexity theory have focused on attractors as a pattern of behavior within a phase space toward which dynamic, nonlinear systems gravitate. Four attractor types have been distinguished: point, cyclic, torus, and strange. In the case of the torus attractor there is a high degree of irregularity and complexity in the pattern, particularly when compared to the point or circuit attractors. But unlike the strange attractor, predictions can still be made, the pattern is fixed and finite. When there is more than one frequency in the periodic trajectory of the system through the state of a limit cycle, the trajectory will no longer be closed, and the limit cycle becomes a limit torus (namely if two of these frequencies form an irrational fraction and are therefore incommensurate). The system, therefore, approaches two different points periodically but does not escape that cycle. Torus-shaped cyclic attractors represent first-order change and have a dimension of 2 (a surface).

As a torus continues to move farther away from its periodic, ellipsoid cycle, it collapses into two or more tori. This creates two outcome basins which take the form of a butterfly -- thereby constituting a second-order change. The transition from a torus to chaos has been intensively investigated. Two types of instabilities exist, which cause the collapse of tori: One is in the phase direction and the other in the amplitude direction [more]. Strange attractors, as indicators of chaotic systems, are said to exhibit third-order change, since the periods of these systems have bifurcated for the third time. It may be asked whether human values should be understood as torus attractors or strange attractors (cf Human Values as Strange Attractors: Coevolution of classes of governance principles, 1993).

Attractors are now being associated with processes of the mind (cf David Abraham, Chaos, Bifurcations and Self-organization: dynamical extensions of neurological positivism and ecological psychology, 1996). The challenge may be to understand how loss of coherence is associated with what is described in mathematical terms as the decay of correlations for the automorphism of the torus, notably due to chaotic mixing (cf Decadent Dynamics : Suggested papers) [more]. The challenge of loss of coherence in psychosocial systems may then be understood as "torus decay" -- potentially a major challenge for efforts towards sustainability (cf Psychology of Sustainability: Embodying cyclic environmental processes, 2002). The challenge of torus decay is central to the successful management, namely the sustainability, of plasma in nuclear fusion reactors as noted by E. Coomer et al (An experimental and computational study of compact torus formation, decay and heating in the Berkeley Compact Torus Experiment, Nuclear Fusion 40, 2000, pp. 1669-1681).

It might also be asked whether the challenge of torus decay could be usefully understood as fundamental to psychosocial coherence as exemplified by social memory (cf Societal Learning and the Erosion of Collective Memory: a critique of the Club of Rome Report, 1980) or in a society's response to its environment (cf Jared Diamond, Collapse: how societies choose to fail or succeed, 2005). Is there a degree of isomorphism with the challenge of "fault tolerance" in computer memory (cf R. A. Ayoubi, et al Fault Tolerant Hopfield Associative Memory on Torus, 18th IEEE International Symposium on Defect and Fault Tolerance in VLSI Systems, 2003)?

Resonant associations and comprehension of feedback vital to sustainability

Whilst sustainability in response to perturbation may be described satisfactorily in terms of the mathematics of invariant tori, the challenge remains as to how coherence is to be comprehended and sensed as a meaningful attractor in psychosocial systems. Information may indeed be organized in terms of a higher number of dimensions -- beyond strategic management using prioritized "laundry lists" or insights from matrix presentations. But the applications of complexity theory to governance have as yet been of limited significance -- even in response to the complex security problems of terrorism.

It is perhaps useful to return to the distinctions now made between: data, information, knowledge and wisdom:

For an electro-mechanical or biological system, "fault tolerant" sustainability can be ensured by appropriate flows of data through feedback loops. The situation becomes more problematic in social systems when there is a need for fault tolerance in the movement of information through feedback loops. It is here that any erosion of social memory may prove critical. This is even more the case with respect to knowledge and any failure to encompass coherently the requisite variety of factors in arriving at a strategic conclusion (cf Coherent Policy-making Beyond the Information Barrier, 1999) . This failure might be understood to be the tendency towards societal collapse identified by Jared Diamond.

Given the inadequacies of interdisciplinary and transdisciplinary patterns of communication, especially in academic and governance settings, feedback loops vital to psychosocial sustainability tend only be recognizable and cultivated through what might be termed the "resonant associations" typical of cross-boundary creativity. Hence the counter-intuitive importance of metaphor (cf Metaphors as Transdisciplinary Vehicles of the Future, 1991; Documents relating to Metaphor for Governance) and the arts (cf Poetry-making and Policy-making: arranging a marriage between Beauty and the Beast, 1993; Aesthetics of Governance in the Year 2490, 1990). The challenge is however that, whilst associations may be intellectually recognizable, as a coherent pattern capable of sustaining a psychosocial system, they call for a degree of psychological ("enactive", "embodied") engagement that may be inadequate. Hence the increasing concern with requisite "wisdom" (cf Human Values Project: Wisdom and Requisite Variety).

It is unfortunate that contemporary understandings of "wisdom" have yet to be given any operational form relevant to the sustainability of psychosocial systems (cf Council of the Whys: emergent wisdom through configuration of why-question dynamics, 2006). The periodic use of "Councils of the Wise" (especially "Wise Men") has not been widely significant in its outcomes, nor have attempts to connect with indigenous wisdom traditions (cf "Wisdom Keepers"). The interactions between those of different persuasions, who are acclaimed as "wise", have also tended to be disappointing in terms of expectations (especially in the case of interfaith dialogue). The intensified focus on "leadership" has been effectively divorced from any requirement for "wisdom" -- exemplified by the quality of leadership of the countries represented in the United Nations Security Council, itself not renowned for "wisdom".

If "wisdom" is to be relevant to psychosocial sustainability, there is perhaps therefore a case for recognizing it in two forms:

There is therefore a possibility that the necessary coherence may be sustained through a "pattern of resonant associations" that could be best understood as mapped onto a torus -- understood both as an "objective" mapping surface and as a "subjective" mnemonic device, or lens, through which understanding may be self-reflexively and emergently ordered. The latter use necessarily requires a degree of internalization or "embodiment of mind" through which the torus becomes a vehicle for the dynamic expression of identity (cf Francisco Varela, et al. The Embodied Mind: cognitive science and human expression, 1991). The meditational disciplines in relation to the use of mandalas are an example -- just as the unreconciled special claims for particular spiritual disciplines are a caution.

http://www.imageandnarrative.be/mediumtheory/michaelschiltz.htm

http://www.imageandnarrative.be/inarchive/mediumtheory/michaelschiltz.htm

Beyond the plane: form and medium in terms of the calculus of indications

In contrast to the plane surface of a simple matrix, a torus holds an interesting position in the discussion of the relationship between form and medium as fundamental to advanced theories of communication. This notably featured in the work of Niklas Luhmann (Die Gesellschaft der Gesellschaft, 1997) and discussed by Michael Schiltz (Form and Medium: a mathematical reconstruction, Image [&] Narrative, 6, 2003) in relation to the calculus of indications of George Spencer-Brown (Laws of Form, 1969/1994). Schiltz notes that form/medium is "the image for systemic connectivity and concatenation", as described by Humberto Maturana and Francisco Varela. Schiltz notes, that the notion of "space" is the key to reflexivity appropriate to any discussion of form and medium, citing Spencer-Brown as follows:

In all mathematics it becomes apparent, at some stage, that we have for some time been following a rule without being aware of it. This might be described as the use of a covert convention. [… Its] use can be considered as the presence of an arrangement in the absence of an agreement. For example, in the statement and theorem.... it is arranged (although not agreed) that we shall write on a plane surface. If we write on the surface of a torus the theorem is not true […] The fact that men have for centuries used a plane surface for writing means that, at this point in the text, both author and reader are ready to be conned into the assumption of a plane writing surface without question. But, like any other assumption, it is not unquestionable, and the fact that we can question it here means that we can question it elsewhere […]

A somewhat related point has been made by R Buckminster Fuller (Bias on One Side of the Line In: Synergetics: explorations in the geometry of thinking, 1975, #811.00). What are the implications of the added emphasis above for elaborating psychosocial development strategies?

Schiltz then comments (in language that calls for a longer quotation to convey the richness of the subtle argument -- emphasis added) :

It was our choice to write in a plane surface that has made that distinctions indeed do cut off an inside from an outside, that 'differences do make a difference' (Gregory Bateson). Covert conventions at a level deeper than the level of form, preceding the level of form, have determined what the form would do. There lies a chance for developing a medium theory here. In this concrete case: the medium of the plane surface makes the difference. And in general: the topology of the medium makes the difference between distinctions making a difference and distinctions not making a difference. 'It is now evident that if a different surface is used, what is written on it, although identical in marking may be not identical in meaning"... Spencer-Brown has shown us that the 'medium is the message' (Marshall MacLuhan).....

Spencer-Brown's solution to the problem of many-valued functions is well-known. He constructs a tunnel 'subverting' the plane, and connects the distinguished sides. As hinted to above, the topological qualities of space are thus altered. We are now writing in a space that grants a form the possibility of access to itself, yet denies the possibility of identity with or presence to itself (Michael Schiltz and Gert Verschraegen, Spencer-Brown, Luhmann, and Autology. Cybernetics and Human Knowing 9, 2002, 3-4). Hence, we are writing in a space that connects the level of first-order (operand) and second-order (operator) observations. That space is a torus. If considered operationally, distinctions written on a torus can subvert their boundaries and re-enter the space they distinguish, turning up in their own form. The marked state cannot be clearly distinguished from the unmarked state anymore, leading to the 'indeterminacy' of the form. As the calculus explains, the state envisaged as such is a state not hitherto envisaged in the form. It is neither marked nor unmarked. It is an imaginary value, flipping between marked and unmarked, thanks to the employment of time. The form of the re-entry, as described here, has been the source of many commentaries....

Such conceptualization diverts sharply from an intuitive understanding of a medium. As seen here, a medium is far from a Euclidean container. Rather is it introverted space, it is identical to the topology of the form, it is the form's 'deep structure'.

There is at least the possibility that shifting out of planar articulation of any "peace process" in the Middle East, for example, might clarify more coherent options.

Schiltz concludes:

If the medium of meaning is indeed the ultimate medium of psychic and social systems, i.e. if meaning is 'the medium of itself', then what is its 'form', the distinction through which it can be expressed? I perceive only one answer: the medium of meaning must be identical to the difference between form and medium, and the re-entry of that distinction into itself. Its consequent indecidability is the symbol of our dealing with the world. It expresses the fact that all our attempts to get a hold of the world are doomed to frustration.... Meaning as our phenomenology of this world can only be partial, as the difference between form/medium can only be actualized as a form. In mathematical terms: meaning is a lambda-domain occupied by communications that, by acting on themselves (= being a function of themselves), produce new communications in the same domain which can in turn act on themselves and further expand the domain. [cf Louis H. Kauffman, The Mathematics of Charles Sanders Peirce, Cybernetics and Human Knowing, 8, 1-2, 2001]

The theoretical usefulness of the distinction (and potentially its significance for sustainable development) is demonstrated by Schiltz through the exemplary medium of money:

No other medium is so clearly de-ontological. There is no identity in money, it is never present to itself, as it surrenders to the functional instability of valuation; and what else is valuation but the economic description of the circulation of money in and by the system of the economy? ....In other words: the system of the economy enlivens and reproduces the difference between form (payment) and medium (money) at all times controlling or conditioning the difference by means of prices (signals for expectations of payments).... The medium of money allows the perspective in economic operations, without being fixed or stuck in a certain state, (let alone being consumed at any moment), but also without ever being observable as medium. The medium is the ever present, yet non actual (!) surplus inherent in each and every present and actual form, it is comparable to a horizon shifting with each and every systemic operation...money is itself only by virtue of adapting to separate individualities (forms)....

For Niklas Luhmann, the problem is to describe self-referentially operating social systems, consisting of operations which take their own results as a base for further operations. These are forms that 'in-form' themselves, indeed. Two-valued logic cannot provide a conceptualization here, for a reason that is clear: limiting itself to the possibilities of the plane space, it cannot indicate an observer. With Joseph Schumpeter, we must only think of the example of money creation in the economy to realize the large insufficiencies of two-valued logic to describe the intricacies of this process ...

In order to guarantee connectivity, and this certainly means as well: in order to reconstruct the function of money!, the difference between payment and non-payment must be reconstructed so to enable future payments, in order to enable future form.

It is widely accepted that no economist questioning assumptions regarding these monetary foundations can expect to be assured of a future in that discipline or in the institutions employing such expertise. (cf Peter Koenig, 30 Lies About Money: liberating your life, liberating your money, 2003). In practice, however, these assumptions are questioned in the operation of over 1,000 complementary currency systems.

The general argument raises the question of the impact of paper and flat computer screens (and "pull down" menus) in undermining any desirable emergence of non-planar surfaces for the presentation of information more capable of enabling and enhancing sustainable development. Perhaps there is a case for the "crystal balls" of the futurists of yore! The challenge is particularly evident in the articulation of any "global ethic", strategic "vision", mission statement or global plan -- like Agenda 21 (cf Structure of Declarations Challenging Traditional Patterns, 1993; Distinguishing Levels of Declarations of Principles, 1980 ). What would be the consequence of endeavouring to articulate these on a torus?

Related questions of interest are to be found in the philosophical discussion of closure by Hilary Lawson (Closure: a story of everything, 2001). He notes that "things" occur with closure:

Closure can be understood as the imposition of fixity on openness....It is the conversion of flux into identity, the conversion of possibility into the particular." Lawson uses a simple example of a piece of paper with many random dots on it. From that, we can perceive various patterns, lets say we can identify a face. That face - that 'thing' - is the result of a closure. The world of things, the world of chairs, music, quarks, algebra, society, and so on, are the results of closures. And, typically, closures are stacked upon other closures. For example, 'paper' and 'dots' are also the results of closures upon which the result of closure of 'face' rests. It is immediately clear, also, that closures incorporate a context of other closures; at the least, it is a ceteris paribus condition. [more | more]

In considering such closure elsewhere (Psychology of Sustainability: Embodying cyclic environmental processes, 2002), Lawson's position was cited as follows:

Instead of seeing the world as a thing, a universe, whose truths we might uncover through for example the procedures of science, Closure proposes that we regard the world as open and it is we who close it through our stories. The resulting framework offers solutions to the central questions of contemporary philosophy: the character of language and meaning, of the individual and consciousness, of truth and reality. As a theory of knowledge Closure has dramatic consequences for our understanding of the sciences, changing what we think science is about and how it is able to do it. It also accounts for why we need and desire both art and religion. It reshapes our understanding of ourselves and the organization of society, our goals and our capacity to achieve them. But above all it makes sense of where we are and who we are.

To what extent are the various approaches to sustainable development, and the search for alternative paradigms, to be considered as efforts to achieve new -- and more encompassing -- forms of closure?

Resonant association of psychosocial identity with intertwined tori

The question requiring consideration is how psychosocial coherence and identity is characterized by a pattern of associations that can best be mapped onto a single torus -- or onto intertwined tori -- to ensure a degree of stability under perturbation. A number of pointers exist:

Cybertextuality: According to Ian Lancashire (Cybertextuality, TEXT Technology, 2, 2004 ):

Cybertexts are the pairs of utterance-message and feedback-response that pass from speaker-writer to listener-reader, and back, through a channel awash with noise. Cybertextuality is a broad theory of communication that draws on the cybernetics of Norbert Wiener (1894-1964) to describe how we manage these dual message-feedback cybertexts into being and that helps explain the publishing, the transmission, and the reception of all speech and text. Recursiveness, complexity, and homeostasis are three principles of cybertextuality. Because we are cognitively blind to how we create most utterances (language belongs to procedural memory, which can be recalled only by enacting it), we unselfconsciously model even our own language acts (not just ones by other people) simply in order to recognize and revise them. We observe or receive our own language acts before anyone else does. Our feedback is to represent those acts meaningfully. Mental modelling, as a feedback mechanism, is recursive. Our every utterance or output serves as input to another (possibly silent) uttering.

This approach is related in interesting ways to the above arguments of Schiltz in points subsequently made by Lancashire (emphasis added):
By externalizing our working-memory onto paper or screen, we model and give feedback on not only our inner voice, which falls into working memory, but also visual text, remediated speech. We manage or steer composition composed silently and then written on the page, or to a computer file and screen, by means of two almost overlapping cybertextual cycles. The cybernetic channel, metaphorically, resembles a twinned torus. Our mind must model two received cybertexts: the inner voice (received instantly), and its re-mediation as visual input through the eyes (received after cognitive recoding into auditory form). We use both slave systems of working memory at once. Cognitively, our receiving attention is divided. The more functions that an external working-memory system has, the greater the possibility of conflict between the models that the mind makes.

Accounting: Accounting is a fundamental tool in the management of systems integral to sustainable development. Conventional accounting is based on methods of double-entry bookeeping using common spreadsheet software applications -- extended into input-output analysis, notably for macro-economic modelling. A proposal was previously made for an accounting system based on a spherical metaphor (Spherical Accounting: using geometry to embody developmental integrity, 2004). This considered in passing the transition from spreadsheet to torus. It is possible that much more could be derived from a toroidal metaphor (note, for example the existence of an accounting application named Torus Systems). To the extent that sustainability can be understood as balanced input-output, and sustainable development can be understood as a particular form of sustainable of imbalance in input-output, there is a case for determining whether sustainable development could be better understood in terms of a toroidal model.

Multi-agent modelling and sustainable development: With respect to the Scientific Support Plan for the European Commission's Environment and Sustainable Development Programme, P-M. Boulanger and Th. Bréchet (Setting concepts into motion: improving scientific tools in support of sustainable development decision-making, 2002) point out:

One of the main shortcomings of system dynamics models lies in the immutability of their structure... The new-generation system theory, called 'complex system theory'..., tries to overcome these limitations. Multi-agent models belong to this new generation of complex system models.... These models mainly simulate (by way of computer programs) whole populations of autonomous agents interacting with each other inside an artificial environment. The latter is generally reduced to a very abstract structure of elementary cells (lattice, torus) equipped with a limited set of dynamic properties (stocks of resources, absorption capacity for a pollutant, etc.), but nothing prevents a modeller from representing more realistically real territories with their geological, ecological, or social properties.

Agent-based computational models have enabled exploration of questions of sustainable development on the surface of a torus as in the work of A. Janssen and Elinor Ostrom (Adoption of a New Regulation for the Governance of Common-Pool Resources by a Heterogeneous Population; Critical Factors that Foster Local Self-Governance of Common- Pool Resources: the role of heterogeneity, 2001).

In the study by Petia Manolova (Exchange fluxes, expectations, and risk aversion in a multi-agent economy, 2005):

We consider an economy consisting of a finite number of agents located on a one-dimensional torus. Time is discrete. The agents interact sequentially. Each agent buys a vector of goods from its left neighbour, produces some other goods, sells goods to its right neighbour and consumes the rest. Thus, there are two opposite fluxes on the torus - goods and money. Each agent attempts to maximize a scalar constant risk aversion utility function of the expected produced and consumed quantities w.r.t. its production and exchange decision, subject to different instantaneous and intertemporal balance requirements. Information is local - each agent knows only the history of its own buy, sell, and production decisions.

Simulation of social connectivity: A torus is often assumed as the fundamental form via which connectivity can be explored, especially in the light of the recognition in computer development that a torus network has better dynamic communication performance than an ordinary mesh network [more]. Simulations of such connectivity are effectively a special case of multi-agent modelling:

Gossip networks: The role of gossip in sustaining and developing relations in a network of people has been modelled by Márk Jelasity (Engineering Emergence through Gossip, 2005), demonstrating convergence on a torus pattern. He argues that the result of gossip is that new and interesting information spreads over a social network not unlike diseases during an epidemic, or computer worms over the Internet. As a periodic information exchange among members of a group over a network that connects them, and a subsequent update of the knowledge of the group members based on the information they exchange, gossip is a powerful abstraction that can be applied for solving a wide range of problems in distributed computing.

Emergence of social norms: The role of a torus in constraining the emergence of social norms has been explored by Cees Withagen (Evolution of social norms in a spatial common resource pool game).

Sustaining cooperative regimes: Michael D. Cohen et al. (The Role of Social Structure in the Maintenance of Cooperative Regimes, Rationality and Society, 2001)

Small worlds: The contact process in the study of "small worlds" makes notable use of a torus (cf A. D. Barbour and Gesine Reinert, Small Worlds, 2002; Rick Durrett and Paul Jung, Two Phase Transitions for the Contact Process on Small Worlds, 2006). This is distinguished from the small world hypothesis whereby everyone in the world can be reached through a short chain of social acquaintances [more]. The concept gave rise to the famous phrase six degrees of separation [more]

Toroidal organization: Curiously, despite the above, there is apparently little research into the structuring of a group or community as a torus, despite the arguments for communication efficiencies -- and the challenge of team breakdown. It would appear to be an interesting way of extending beyond hierarchical structures and networks and potential ideal for communication protocols between individuals in a virtual community -- as a development beyond "web rings". By contrast, toroidal organization is common in microbiology -- as with lipids and proteins and the organization of the genome (circumferential DNA wrapping), and notably in bacteria.

One singular exception is a study, edited by Douglas V. Johnson II (Future Leadership, Old Issues, New Methods, 2000) for the Strategic Studies Institute of the U.S. Army War College. Ironically that body reports to the Pentagon, one of the few institutions within an architectural resemblance to a torus [more]. The study notes that:

In a Torus organization rules, regulations and codes of behavior will maintain order and discipline. In this system linear order is preserved, and continuity is ensured. Uniform regulations apply to everyone without favoritism. Management is kept busy issuing new rules and regulations and ensuring they are observed. Most regulations are in written form, and arrangements of supervision and control ensure enforcement. This type of organization functions best in a stable environment where little change takes place, such as during the Cold War. Weaknesses become apparent in a turbulent environment: lack of ability to change; lack of resilience; and uniform procedures unsuitable to people who are very different from each other. The challenge a Torus leader faces in turbulent times is not how to maintain order and enforce the regulations, but how to create conditions that nourish the growth of change, innovation, enterprise, and creativity. Encouraging renewal and positive change should be the organizational goal.

The study distinguishes the torus mode from complex systems, modelled by "butterfly behaviour", which often behave "like multiple Torus systems joined together. People acting within one group are behaving similarly to one another, but differently than those in other groups". It argues that "Systems that adapt best to changing environmental conditions function mainly in the complex pattern". The question to be asked is how is such complexity to be distinguished from unsustainability and how is any sustainable mode of organization to be implemented if the complex system is incomprehensible to the majority of its members -- except to the extent that they may be perceived to behave like "butterflies", with a half-life to match. If what might be described as institutionalized attention deficit disorder proliferates under the banner of chaos and complexity, how is any form of coherence to be recognized and by whom? How is sustainability to then be ensured?

Psychocultural symbol sets forming a torus: The classical example of a complex cultural coding system is that of the I Ching -- an early inspiration to Leibniz. The binary coding system has been a continuing stimulus to reflection. Together with the Tao Te Ching, the code structure has been applied and reinterpreted in many ways (Hyperspace Clues to the Psychology of the Pattern that Connects in the light of the 81 Tao Te Ching insights, 2003; 9-fold Higher Order Patterning of Tao Te Ching Insights: possibilities in the mathematics of magic squares, cubes and hypercubes, 2003). One stream of reflection has explored the relationship of the I Ching pattern to the genetic code (M Schonberger, The I Ching and the Genetic Code, 1976; K Walter, The Tao of Chaos: DNA and the I Ching, 1994)

In this connection, it has also been recognized that a tabular representation of the I Ching can be read both vertically and horizontally. But additionally the left edge wraps around and attaches to the right edge, and the top folds and joins the bottom -- thus forming a torus (Chris Lofting, The I Ching and the Brain, 1998). This was also envisaged elsewhere ( Networking Alternation: an alternation network of 384 pathways of organizational transformation interpreted for networks in the light of the Chinese Book of Changes, 1983).

The wrapping of magic squares to form a torus has been discussed by John C. Gonsowski (Personality, Physics and Spirituality: a common geometry, 2001) and by Peter D. Loly (A Logical Way of Ordering the Hexagrams of the Yijing and the Trigrams of the Bagua, The Oracle - the Journal of Yijing Studies, 2, 12, January 2002, pp.2-13).

Energy: Implications for toroidal energy dynamics are explored in the development of the torus coil design concept of Marko Rodin (Aerodynamics, 1994), as now promoted by RodinAerodynamics.org [more | more]. This work is extensively based on number theory and the toroidal organization of numbers -- Vortex-Based Mathematics Toroid Surface Topology. The coil is a toroidal form wound by wires in a pattern consistent with newly discovered number patterns. Although toroidal shapes wound with wires are commonly used for inductors in electrical circuits, often for use in transformers, the pattern of winding in this case is radically different from conventional toroidal coils and an unusual range of energy applications are envisaged. According to Scott C Nelson (2001):

Rodin's torus is a precise description of the spatial and temporal harmonics inherent in the formation of plant life forms. These patterns appear to be governed by the spiral series of musical overtones that interact in a system of digital circuitry that can be best described as a toroidal lattice.

Memorability: musical clues to psychosocial system sustainability

The relation of music to the functioning of the brain is a theme in the cognitive neurosciences [more]. Research by Petr Janata et al (The Cortical Topography of Tonal Structures Underlying Western Music, Science, 13 December 2002, 298. 5601, pp. 2167-2170) has indicated that knowledge about the harmonic relationships of music is maintained in the rostromedial prefrontal cortex providing a stronger foundation for the link between music, emotion and the brain. The melody used experimentally was crafted to shift in particular ways through all 24 major and minor keys. The relationships between the keys, representative of Western music, create a geometric pattern in the form of a torus (see Petr Janata, Music Mapped to the Torus, 2005, and torus dynamics movies).

The piece of music moves around on the surface of the torus offering a means of determining the pure representation of the underlying musical structure in the brain. The work clarified the mapping of melodies in the brain, as it varied from one occasion to another suggesting that the map is maintained as a changing or dynamic topography. This dynamic map may provide the key to understanding why a piece of music may elicit different behaviors at different times [more more] (see also Robert J. Zatorre and Carol L. Krumhansl, Mental Models and Musical Minds, Science, 13 December 2002: 298. 5601, pp. 2138-2139). Of particular interest was the role of any such mapping in the memorability of favourite tunes.

The torus may be used as a representation of harmonic space. A piece of music moves around in this space [more]. The results of psychoacoustic experiments by C L Krumhansl and E J Kessler (Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys, Psychological Review 89(4), 1982, pp. 334-368) of the inter-key relations of all major and minor keys can be represented geometrically on a torus -- as shown by Benjamin Blankertz, Hendrik Purwins and Klaus Obermayer (Constant Q Profiles and Toroidal Models of Inter-Key Relations -- ToMIR, 1999) in the following image

Geometric representation of the inter-key relations
of all major and minor keys
(derived from psychoacoustic experiments by Krumhansl and Kessler)
Toroidal representation of inter-key relations in music

Thomas Fiore Music and Mathematics; Beethoven and the Torus) addresses one of the central concerns of music theory, namely to find a good way to hear a piece of music and to communicate that way of hearing. He notes that music theorists make much use of mathematics in creating conceptual categories enabling them to develop taxonomies and classifications of the various sets that arise in music. In particular he shows how group theory offers a way of describing the ways that sets and pitches relate and how they can be transformed from one to another. Fiore focuses in particular on the musical relevance of the PLR group:

This is a set of functions whose inputs are major and minor chords and whose outputs are major and minor chords. These musical functions go back to the music theorist Hugo Riemann (1849-1919). As a result, the PLR group is sometimes called the neo-Riemannian group [see also Edward Gollin, Neo-Riemannian Theory, 2005].

Using the PLR group Fiore shows that the harmonic progression in the second movement of Beethoven's Ninth Symphony traces out a path on a torus. Beethoven's Ode to Joy (in the fourth and ninth movement of that symphony) has been adopted as the official anthem of Europe (Council of Europe, 1972; European Union 1985). Given the passing recognition by the European Commission of the role of the torus in multi-agent modelling relating to sustainable development (see above), it might be asked whether a key to sustainability for Europe lies not "under the noses" of policy makers but rather "behind their ears". Of course there is indeed the possibility that odour may play an unsuspected role as suggested by Chris C. King (Fractal and Chaotic Dynamics in Nervous Systems, 1991) and may also be usefully mapped onto a torus. There may be unsuspected higher orders of significance to references in political discourse as to whether strategies "stink" or "smell right"!

In a helpful overview Justin London (Some Non-Isomorphisms Between Pitch and Time, Music Theory Midwest, April 2001) points to the recognition of the role of the torus by Brian Hyer (Re-Imagining Riemann, Journal of Music Theory 39(1), 1995, pp. 101-38) and Richard Cohn (Neo-Riemannian Operators, Parsimonious Trichords, and their Tonnetz Representations. Journal of Music Theory, 41(1), 1997, pp. 1-66). The tonnetz on which he focuses is a tonal lattice invented by Hugo Riemann as a model for just intonation. He notes that:

Music theorists are not alone in recognizing the torroidal shape of tonal space. Researchers in music perception and cognition have empirically measured the goodness-of-fit for notes and chords in a tonally-primed context, and they too have mapped tonal space onto the surface of a torus.

London concludes:

... metric space is planar, tonal space is non-planar; therefore the two spaces are non-isomorphic. And if the two spaces are non-isomorphic, then there are fundamental problems in trying to map elements or relationships (i.e., functions which employ those elements) from one space to another....What is gained in this exercise is that by trying to follow the same "rules" in constructing graphic representations of tonal and metric relationships, we are forced to confront the differences between them. We also are reminded of how the topologies of ... the metric tree and the tonal tonnetz -- arise from the combination of formal relationships among their component elements as well as the way human beings hear and understand those relationships. As in all of our musical representations, what we can hear and what we can imagine are intertwined and interdependent.

Given the remarkable sustainability of religious orders, monasteries and ashrams, it is worth exploring the role that regular use of bells -- audible throughout the community -- have played in ensuring coherence. Such possibilities are linked to understandings of the cognitive organization associated with any understanding of "attunement" in relation to individual or collective meditation (as well as to the torus-like halo associated with holy people, and even a particular form of clerical tonsure).

Is it possible that particular patterns -- mappable onto a torus -- are more appropriate to ensuring community sustainability? What is to be learnt from bell tuning in ancient China in this respect -- in sustaining scattered communities within the imperial domain? Especially noteworthy was the function of the Yellow Bell in ancient China -- a carefully tuned instrument upon which all other pitches and measurements were based, which was carefully reworked by every new emperor [more | more]. Might this be a key to the challenges of development in Africa (cf Knowledge Gardening through Music: patterns of coherence for future African management as an alternative to Project Logic, 2000)

Possible immediate applications of relevance to sustainability

As noted at various points above, there is a strong case for pursuing research on policy options mapped onto a torus rather than onto a planar surface. Examples of such work include that of Ian S. Lustick (Identity Politics, Globalization Pressures, and Regime Performance in the Middle East: an agent-based simulation and analysis, 2001). Of related significance, given the above-mentioned application to mapping the gun-control debate onto a torus, is the possibility of mapping the perspectives relating to terrorism onto a torus in order to take them out of planar space into a different context where new options may become apparent (cf And When the Bombing Stops? Territorial conflict as a challenge to mathematicians, 2000). Potentially of even greater interest is the possibility of mapping the dynamics that ensure the decay of a sustainable peace process into a chaotic situation.

More generally there is a case for using the data on networks of world problems and strategic options gathered for the Encyclopedia of World Problens and Human Potential to explore ways to map it onto complementary tori. Of particular interest would be the determination of (resonant) configurations of minimum distance between the nodes and the advantages for comprehension over mesh network visualizations. There is, for example, the possibility of mapping the elements of Agenda 21 from the 1992 Earth Summit onto a torus -- a theme evoked elsewhere (Living Differences as a basis for Sustainable Community Ecosystemics of designing, configuring and driving a difference engine to avoid quenching enthusiasm, magic and the life of the spirit, 1998).

Such a mapping might:

The art of governance, like that of breathing, may perhaps best be understood in terms of a self-sustaining torus. Kenneth MacLean, arguing that the torus offers and excellent image of self-awareness, points to speculative work, by Arthur Young (The Reflexive Universe: evolution of consciousnessand, 1974) and others, on the torus as a model of consciousness:

The geometric shape used to describe the self-reflexive nature of consciousness is the torus. The torus allows a vortex of energy to form which bends back along itself and re-enters itself. It 'inside-outs', continuously flowing back into itself. Thus the energy of a torus is continually refreshing itself, continually influencing itself. [more]

Like a smoke-ring, it maintains its form through the cyclic movement at each point of its circumference. A torus thus offers an interesting metaphor of self-possession -- with an empty, or virtual, centre [more]. Arthur Young's insights into this have been represented as a hypersphere [more].

Choosing the dimensionality of living

The mathematician Ron Atkin (Combinatorial Connectivities in Social Systems, 1977) is recognized for relating cohomology in physics and q-connectivity in social science, notably in terms of simplicial complexes. He raised the question of the dimensionality of the knowledge space which people inhabit in terms of their comprehension of their connectivity (Multidimensional Man: can man live in 3-dimensional space?, 1981) (cf Comprehension: social organization determined by incommunicability of insights).

A number of indicators above point to the possibility that people can "inhabit" -- or may already be effectively inhabiting -- a space of higher dimensionality than that of which they are consciously aware. Lacanian topology offers one extreme perspective. Chaos theory and complexity science offer a more dynamic framework -- as has catastrophe theory. Chris Lucas (Complex Living Tensegrities, 2006) argues that people can, and do, live through a particularly structured dynamic. Creativity is now envisaged in terms of more complex spaces and forms (cf Carlo H. Séquin, Analogies from 2D to 3D Exercises in Disciplined Creativity, 1999). Games are played on more complex spaces (cf Torus and Klein Bottle Games). Many multidimensional media effects are now used to sustain imaginative capacity to navigate complex spaces. This might be considered a major role of music -- with the use of iPods to enable a different framing of reality. In his widely cited study M. Scott Peck (A Different Drummer: community-making and peace, 1987) effectively points to the possibility of organizing one's life according to a different rhythm, if not a different melody.

If a man does not keep pace with his companions,
perhaps it is because he hears a different drummer.
Let him step to the music which he hears, however measured or far away.
Henry David Thoreau

Such contexts offer different kinds of connectivity with elements of knowledge, with aesthetic associations, or with people who can share those environments and the particular communication coherence they offer. At one extreme this may simply take the form of unusual kinds of humour. Alternatively it may focus more on a metaphoric construct as originally explored in the classic by George Lakoff and Mark Johnson (Metaphors We Live By, 1990) and in their subsequent work. It may emphasize drug-induced or mystical experience. It may be of relevance to collective governance (cf Metaphoric Revolution: in quest of a manifesto for governance through metaphor, 1988)

More generally such pointers raise the question as to the degree to which people can consciously choose the dimensionality of the space in which they live. Some will indeed argue that any such choice is delusional and possibly difficult to distinguish from the condition of those medically certified to be deluded or even insane. Arguments in support of the social construction of reality -- and the curious belief frameworks of many cultures and sub-cultures, now and in the past -- favour the possibility of such a choice rather than denying it.

The question is then with what freedom people can take modest steps to live individually or collectively in spaces of higher dimensionality. The arguments above of Michael Schiltz (Form and Medium: a mathematical reconstruction, 2003) regarding the choice we make point to the significant consequences of such a choice, if only with respect to money. He compares the dimensionality of paper with that of a torus.

The question may be framed as what indeed stops people from shifting to a different spatio-temporal framework -- provided that they can interface successfully with that of any simple popular consensus (cf Reinventing Your Metaphoric Habitat, 1992). Alternatively, as implied by Lacan, many may already inhabit surprisingly different topologies with very different dynamics -- offering them advantages in their handling of their energy (with possible consequences for their health as Taoists have always understood). The focus here on the torus is therefore one that is less radical than many others and is possibly more accessible to the imagination -- especially given widespread understanding of the form.

Potentially problematic consequences

It is appropriate to be vigilant regarding potentially problematic consequences of adoption of approaches advocated here.

The consequences derive in part from a lower-dimensional response to any higher-dimensional significance associated with a torus-based mapping. A typical response of this kind would be the use of intellectual property legislation to restrict use of mappings on lower-dimensional forms through copyright, patents or trademarks as a means of restricting access to their higher-dimensional significance (cf Future Coping Strategies: beyond the constraints of proprietary metaphors, 1992).

There is a pathetic irony to this propensity of the human spirit that has been caricatured by the archetypal figure in the Lord of the Rings of Gollum/Sméagol -- with associations to the Golem in Jewish tradition. In the tale it was "Sméagol's" possession of the "One Ring" (capable of ruling all the other rings) that corrupted him and engendered "Gollum" as an "evil" split version of his personality that would destroy any who endeavoured to take the ring away. Dwellers like Gollum, in the caverns of their own "Misty Mountains", are already evident. Any symbolically powerful or magical ring in a folk tale (including the Wagnerian Ring Cycle) may of course be usefully compared with a torus as envisaged above and with the vain possessiveness engendered by higher-dimensional objects as attractors.

This points to the possibility of using such "technology" to ensnare and entrap. The relationship to music discussed above provides reminders of the manipulative use of music in advertising jingles (effectively functioning as modern "spells"), as well as the use of music in psychological operations and interrogation. Matching Gollum, there is Sauron in Lord of the Rings who caricatures the archetypal propensity to seek to rule all others (cf The "Dark Riders" of Social Change: a challenge for any Fellowship of the Ring, 2002). Curiously, in the form of a ring or a torc, the torus is strongly associated with both fidelity (as in bonding rites) and with submission and bondage (as with symbols of ownership and even constraining devices). More curiously, in an increasingly industrialized world, is the proliferation of rings, anklets, bracelets for decorative and other purposes -- and the association with body piercing (ear-ings, nose-rings, etc).

An interesting danger is the extent to which any focus on the torus may reflect, sustain or amplify neurotic, psychotic, obsessional or narcissistic tendencies. As a self-referential form, the vortex of torus dynamics may preclude external reference -- or the capacity to engage with external dynamics. The controversy relating to Lacanian topology (discussed above) could be reviewed in this light -- as with any promotion of the significance of the torus, stigmatized as "New Age" (cf Alan Sokal, et al Fashionable Nonsense: postmodern intellectuals' abuse of science, 1999). But in viewing such preoccupations as the "black hole" of pseudoscience, critics may themselves be part of dynamics to be fruitfully mapped by a torus. It is possible that the very process of sustainable creativity may be associated with dynamics -- both fruitful and unfruitful -- that can be usefully mapped onto the torus or other structures (cf Carlo H. Séquin, op.cit.). This may apply both individually and collectively (cf Dynamically Gated Conceptual Communities: emergent patterns of isolation within knowledge society, 2004).

The self-referential dynamics of "sects" (whether religious, ideological or academic, in the sense promoted by Paul Feyerabend) may merit examination from this perspective. The topological "cut" on a torus to which Jacques Lacan refers as a mark of neurosis (see above) may relate to the "sectional" meaning fundamental to the significance of "sect" in cutting up the body of knowledge and its associated psychodynamics. Whereas the need for appropriate "health and safety" measures has now been well understood in the case of conventional laboratory experiments, it may well be the case that psychosocial experiments, valuable for an emerging knowledge society, call for analogous environments when dealing with unforeseen consequences of exploration of torus and related psychodynamics.

An interesting feature of such problematic challenges to the coherence of sustainability is the nature of the higher-dimensional learnings to which they point -- as typically indicated through the plot development of myths and legends featuring a ring. The core challenge of prevention of quenching, in the management of plasma in torus fusion reactors, clearly makes the point that efforts to "grasp" and "possess" higher-dimensional processes through their lower-dimensional "containers" misunderstand the nature of those processes and their relationship to the understanding vital to sustainability. Both the elusive dimensions to the necessary understanding -- exemplified by the current challenges in managing plasma -- and the widespread occurrence of toroidal processes, suggest that other ways of thinking are called for. Allusions to such understanding are of course made in many folk tales (cf Payam Narbaraz, Simurg: A Persian Fairy Tale).

References

Miguel Carrion Alvarez, Joseph Corneli, Genevieve Walsh, and Shabnam Beheshti. Double Bubbles in the Three-Torus [text]

Margaret Boittin, et al. Math That Makes You Go Wow: a multi-disciplinary exploration of non-orientable surfaces (Written and designed for Math 195a at Yale University). 1998. [text]

Robert Burkhardt:

Davide P. Cervone. The Mathematics of In- and Outside the Torus [text]

B. Crowe. A Complexity Science- Based Theory and Philosophy for Music Therapy Practice and Research. Music Therapy Today, V, 2004, 3 [text]

Antonio de Nicolas. Four-Dimensional Man: the philosophical methodology of the Rigveda. Bangalore, Dharmaram, 1971

Duane Elgin:

Walter J Freeman. Strange Attractors that Govern Mammalian Brain Dynamics Shown by Trajectories of Electroencephalographic (EEG) Potential. IEEE Transactions on Circuits and Systems, 35, 1988, 7 [text]

Eugene A. Grigor'ev. Fundamental properties of toroidal structures with current [text]

John F. Hawley. Global Magnetohydrodynamical Simulations of Accretion Tori [text | simulations]

Daryl Hepting, Gianne Derks, Kossi D. Edoh, and Robert D. Russell. Qualitative Analysis of Invariant Tori in a Dynamical System, 1995 [text]

Daryl Hepting. A Visual Analysis of Invariant Tori. 1995 [text]

W Patrick Hooper. Torus Dynamics [applet]

K Kaneko. Collapse of Tori and Genesis of Chaos in Dissipative Systems. Singapore, World Scientific, 1986 [text]

William Kocay et al. Drawing Graphs on the Torus. Ars Combinatoria, 59, April 2001 [text]

Martin Kraus. LiveGraphics3D Example: Two Interlocking Tori [text]

Erich Jantsch. The Self-organizing Universe: scientific and human implications of the emerging paradigm of evolution. New York, Pergamon, 1980

Anthony Judge:

J. A. Scott Kelso. Dynamic Patterns: the self-organization of brain and behavior. MIT Press, 1995

Chris C. King. Fractal and Chaotic Dynamics in Nervous Systems. Progress in Neurobiology 36, 1991, pp. 279-308 [text]

Hilary Lawson. Closure: a story of everything. Routledge, 2001

John Lilly. Personal Metaprogrammatic Language: an example of its properties [text]

Justin London. Some Non-Isomorphisms Between Pitch and Time Music Theory Midwest, April 2001 [text]

J. M. Lopez and F. Marques. Dynamics of Three-Tori in a Periodically Forced Navier-Stokes Flow. Physical Review Letters, 85, 5, 31 July 2000 [text]

Donald McNeil. A survey of applied systemology. Systems Research, 12(2), 1995, 133-145.

David Mumford, Caroline Series, and David Wright. Indra's Pearls: the vision of Felix Klein. Cambridge University Press, Cambridge, 2002.

Antonio González, Miguel Valero-García and Luis Díaz de Cerio. Mandlebrot Embedding Hypercubes onto Rings and Toruses. 1993

Antonio González, Miguel Valero-García and Luis Díaz de Cerio. Executing Algorithms with Hypercube Topology on Torus Multicomputers. IEEE Transactions on Parallel and Distributed Systems, 6, 1995, 8, pp. 803 - 814 1995 [text]

Lixin Tao, Eva Ma. Simulating parallel neighboring communications among square meshes and square toruses. Journal of Supercomputing, 5, 1, 1991, pp. 57 - 71 [text]

Rajendra Jarga Magar. Toroidal Game of Life II. Grinnell College, 2001 [text]

Takashi Nishikawa and Kunihiko Kaneko. Fractalization of a torus as a strange nonchaotic attractor. Physical Review E, 54, 6, December 1996 [text]

Ole Nelson. Toroidal Game of Life. Grinnell College, 2000.

Robert F. Port. The Dynamical Systems Hypothesis in Cognitive Science, 2001. In: The MacMillan Encyclopedia of Cognitive Science [text]

Robert Port and Timothy van Gelder (Eds). Mind as Motion: Explorations in the Dynamics of Cognition. MITP, Cambridge, 1995.

V A Ryabov. Dynamics on a torus. Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Jan; 71(1 Pt 2) [abstract]

Richard Serra. Torqued Spirals, Toruses and Spheres. Steidl Publishing, 2002

Brian K. Spears and Andrew J. Szeri. A new route to chaos: Sequences of topological torus bifurcations Chaos: An Interdisciplinary Journal of Nonlinear Science, 15, September 2005 [text]

Paul Trow. Dynamical Systems on the Torus, 2003 [text]

Yu-Chee Tseng, Sandeep K.S. Gupta. All-to-All Personalized Communication in a Wormhole-Routed Torus. IEEE Transactions on Parallel and Distributed Systems, vol. 07,  no. 5,  pp. 498-505,  May,  1996. [text]

T. R. Young and James Yarbrough. Reinventing Sociology: missions and methods for postmodern sociology. 1993 [text]

T. R. Young:

Creative Commons License
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

For further updates on this site, subscribe here